La struttura del favo
Nel 1712 l'astronomo Giacomo Maraldi misurò l'angolo di inclinazione dei tre rombi di una cella di api e trovò la misura di 109°28' (Angolo B in ABC v.fig.) e il suo supplemento 70°32'(Angolo C in BCF v.fig.) .
Réaumur, ritenendo che la forma dell'alveolo corrispondesse a un criterio di economia propose il seguente quesito a Koenig
Fra tutte le cellule esagonali a fondo, composte di tre rombi uguali,determinare quella che può essere costruita con il minimo di materia.

E Koenig, nel 1739, mediante il calcolo differenziale trovò che gli angoli della cella di minima superficie erano di 109°26' e il suo supplemento 70°34'. Ma sbagliò i calcoli, vedremo perchè. Mac Laurin nel 1743 confermò i valori di Maraldi.

Segue la dimostrazione geometrica di Mac Laurin

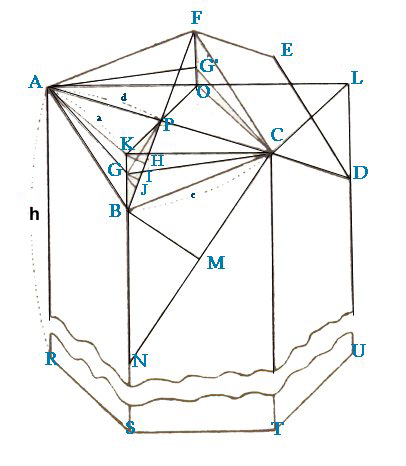Sia F il vertice comune dei tre rombi di lato c che formano il fondo della cella . Sia l'esagono AKCL.. di lato a sezione retta del prisma; il suo centro O sarà la proiezione di F sul piano della sezione.
Uniamo A con C e K con O . Per AC conduciamo un piano che interseca i piani CFO ,AFO ,RABS , SBCT e determina il rombo AG'CG . Sia h =AR l'altezza del prisma e d la semidiagonale AP .
Consideriamo un terzo dell'alveolo, calcoliamo la superficie e vediamo a quale posizione del piano AG'CG essa risulta minima.
La superficie formata dai trapezi RAGS , CGST e dal romboAG'CG , è
(h+GS)a+2d x GP = (h+h-GK)a + 2d x GP = 2ha - a x GK +2d x GP.
Il prodotto 2ha è costante, il problema si risolve rendendo minima l'espressione
[2d x GP + a x GK] (1) .
Posto B su KS in modo che [BK:BP=a:2d] (2) .
Da P come centro e raggio PG , si descriva nel piano BKP un arco di circonferenza che incontra PB in J , si conducano le perpendicolari a PB da K e G .
Dai triangoli rettangoli simili GIB, KHB, BKP e dalla (2) si ricava BI:BG = BH:BK = BK:BP = a:2d per la proprietà dello scomporre delle proporzioni si ha (BH-BI):(BK-BG) = a:2d ovvero IH:GK = a:2d oppure a x GK = 2d x IH
L' espressione (1) si scriverà 2d x GP -2d x IH = 2d(GP-IH)= 2d(JI+HP)
Ma d e HP sono costanti, allora il minimo si ha per JI=0 ovvero quando J e I si confondono, quindi G si trova in B , posta vera la (2) .

da:From Colin Mac Laurin to Sir Martin Folkes 30. June 1743. Therefore is the Rhombus of the most advantagious Form in Respect of Frugality, when KB is to PB as KC is to AC . This is the same Method by which we have elsewhere determined the Maxima and Minima , in the Resolution of several Problems that have usually been treated in a more abstruse Manner. See Treatise of Fluxions Art. 572, &c....

Determiniamo gli angoli dei rombi FABC, FCDE,..
Sia P il punto di intersezione delle diagonali AC e OK del rombo AOCK .
Essendo il triangolo OKC equilatero si ha: KC2=OK2=4PK 2.
L'angolo in K di PKC è di 60° , segue che PC 2=3 PK2 o AC=2PC=2Ö3 x PK.
Di conseguenza si ha KC:AC = 2 PK:2Ö 3 x PK = 1: Ö3 e per ipotesi (2) KB:PB = KC:AC = 1:Ö 3
o PB:PK = Ö 3 : Ö 2 e poiché (PK:PC = 1:Ö 3) allora PB:PC = 1:Ö 2 o PC/PB= Ö 2 .

Ma PC/PB è la tangente trigonometrica dell'angolo B=b/2 di CBP ; b/2 =54°44'08'' da cui l'angolo in B di ABC è di 109°28'16'' e il suo supplemento angolo C= adi BCF è di 70°31'44''= a=2arctan(1/Ö 2 )

Mac Laurin .... that is the Angle CBP is that, whose Tangent is to the Radius as Ö 2 is to 1, or as 14142135 to 10000000, and therefore is of 54°44'08'', and consequently the Angle of the Rhombus of the best Form is that of 109°28'16''

Diamo ora una dimostrazione, più elegante con il calcolo differenziale.
Consideriamo il prisma piatto P con base esagonale e il prisma a vertice V costuito da tre rombi.
Per brevità consideriamo un terzo della cella.
I volumi dei prismi, di altezza uguale a h, P e V sono uguali perchè i tetraedri CBAK e CFAO hanno lo stesso volume per simmetria centrale, ciò che viene tolto viene aggiunto.
Calcoliamo le superfici laterali dei prismi P , V e poniamo il lato AK = KC dell'esagono uguale a 1; quindi AC=Ö 3 .
L'altezza del prisma piatto P è h, sia x = OF = KB .
Si ha AF=FC=CB=BA= Ö( 1+x2) e FB=Ö (1+4x2)
Area totale di (sempre un terzo della cella) P , 2 rettangoli e un rombo, uguale a 2h + Ö 3 /2
Area totale di (sempre un terzo della cella) V , 2 trapezi e un rombo, uguale a 2h- x + Area( FCBA)
Area( FCBA)= 1/2*AC*FB= (1/2)* Ö(3+12x2)
Dunque per un terzo di V si ha la superficie funzione di x --> V(x);
V(x)= 2h-x +(1/2)* Ö(3+12x2) *
Per x=0, ovvero quando B coincide con K si ritrova 2 h + (Ö 3) /2
Con lo studio della derivata prima V'(x) si ha: V'(x)=[Ö(1+4x2) +2xÖ(3)]/ Ö(1+4x2) ,
si trova il minimo per x=(Ö 2)/4
Sostituendo x=(Ö 2)/4 in * si trova per V il valore 2h+(Ö2)/2 che è inferiore a 2 h + (Ö 3 )/2
Quindi con la costruzione dell'alveolo a fondo cuspidato le api risparmiano cera.
Considerando il rombo FABC si ha che FA=FC= 3*(Ö 2 )/2 , per x=(Ö 2)/4, e AC=(Ö3) dunque nel triangolo ABC con il teorema di Carnot si ha cos(ABC)=-1/3 l'angolo ABC misura 109°28'16'' e il suo supplemento BCF 70°31'44''

Koenig sbagliò perchè calcolò le somme parziali dello sviluppo in serie della funzione arctanx fino alla tredicesima potenza, mentre Mac Laurin ottenne il suo risultato arrivando alla diciasettesima potenza
Arctan x = x-(x3)/3+(x 5 )/ 5 - (x7 )/7+....+ [(-1)n-1)* (x 2n-1)/(2n-1)]con |x|<1
Da a/2=arctan(1/Ö 2 )
Calcolando le somme parziali,con Derive o Turbo Pascal si ottengono i risultati in radianti e riferiti a a/2
Le somme parziali fino alla tredicesima potenza ci danno in radianti 0,6157356087 , risultato di Koenig.
Le somme parziali fino alla diciasettesima potenza ci danno in radianti 0,6155298025 ,risultato di Mac Laurin.

Conclusioni.
Abbiamo ricostruito la storia del problema posto da Réaumur, risolto da Mac Laurin. C'è da dire che a parità di volume tra due prismi a facce esagonali la superficie è minima non quando il fondo è costituito da tre rombi con angolo di 'Maraldi' ma se il fondo è costituito da 2 rombi e due esagoni.Problema risolto da F.Toth.
Tóth, L.F. 1964. What the bees know and what they do not know. Bulletin of the American Mathematical Society 70(July):468.
Altre considerazioni.
Alle api va bene la soluzione di 'Maraldi'.
Ma le api perchè costruiscono le celle a forma esagonale e con il fondo a cuspide?
Si potrebbe rispondere con le parole di Plinio."Ogni cella è esagonale, perché ognuna delle sei zampe dell'ape ha fatto un lato". -Sexangulae omnes cellae a singolarum pedum opere-.
Non accettabile,ovvio. Vedremo la spiegazione fisico-matematica in un prossimo articolo.

-----------------------------------------------------------
Bibliografia
The collected letters of Colin Mac Laurin edited by Stella Mills University of Birmingham Shiva Plubbishing Limited pp 386-391
Matematica dilettevole e curiosa Italo Ghersi Hoepli Milano Quinta edizione 1988 pp 556-561


Giacomo Omallini